Understanding LQR: A Comprehensive Guide To Linear Quadratic Regulator
Linear Quadratic Regulator (LQR) is a critical concept in control theory and engineering, providing efficient solutions for optimizing control processes. This article delves into the intricacies of LQR, discussing its principles, applications, and advantages. Whether you are an engineer, a student, or simply someone interested in control systems, understanding LQR is essential for grasping modern control strategies.
In this guide, we will explore the basic principles of LQR, its mathematical foundations, and how it applies to various fields, including robotics, aerospace, and automation. We will also cover practical considerations, including implementation techniques and challenges faced during application.
By the end of this article, you will have a solid understanding of LQR, its importance in control systems, and how to apply its principles effectively. Let's dive into the fascinating world of Linear Quadratic Regulators!
Table of Contents
- What is LQR?
- Principles of LQR
- Mathematical Foundation of LQR
- Applications of LQR
- Advantages of LQR
- Implementation Techniques
- Challenges of LQR
- Conclusion
What is LQR?
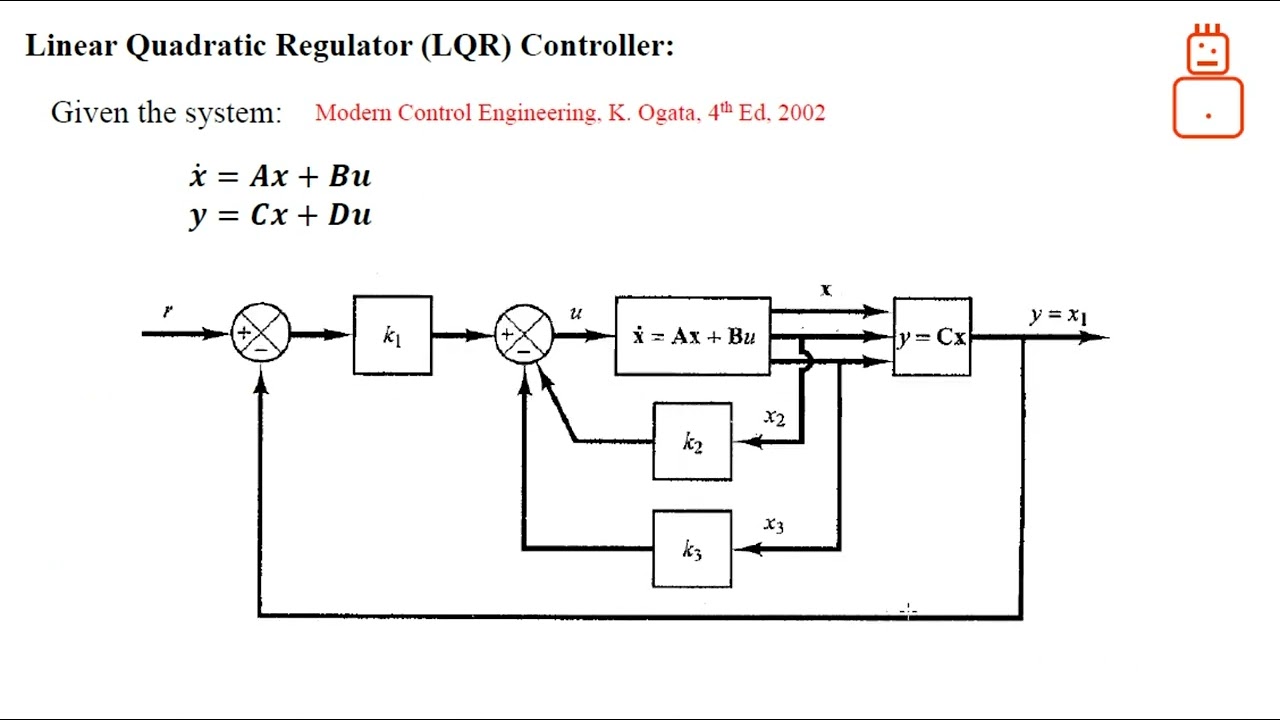
The Linear Quadratic Regulator (LQR) is an optimal control strategy used to operate dynamic systems. It aims to minimize a cost function that is quadratic in the state and control variables, providing a systematic approach to control design. LQR is widely recognized for its effectiveness in stabilizing systems and its ability to handle various constraints.
In essence, LQR formulates a control problem by defining a cost function, which consists of two parts: the state error and the control effort. The goal is to find a control law that minimizes this cost function, resulting in optimal system performance.
Principles of LQR
The principles of LQR are grounded in the concept of state-space representation. The system is described by a set of linear differential equations, and the control input is determined by the state of the system. The fundamental principles include:
- State Feedback: LQR employs state feedback to adjust the control input based on the current state of the system.
- Cost Function: A quadratic cost function is defined, incorporating both the state and control inputs.
- Optimal Control Law: The solution to the LQR problem yields an optimal control law that minimizes the cost function.
Mathematical Foundation of LQR
The mathematical foundation of LQR involves solving a set of linear equations. The state-space representation of a system can be expressed as:
dx/dt = Ax + Bu
where:
- x is the state vector
- u is the control input
- A is the system matrix
- B is the input matrix
The cost function is defined as:
J = ∫ (x^T Q x + u^T R u) dt
where Q and R are weighting matrices that define the trade-off between state error and control effort. The optimal control law is derived using the Riccati equation, which provides the necessary feedback gain to minimize the cost function.
Applications of LQR
LQR finds applications across various fields due to its robustness and effectiveness. Here are some key areas where LQR is commonly used:
LQR in Robotics
In robotics, LQR is employed to control the motion of robotic arms and mobile robots. The ability to maintain stability and accuracy in dynamic environments makes LQR a preferred choice for robotic applications.
LQR in Aerospace
Aerospace applications utilize LQR for flight control systems in aircraft and spacecraft. Its capability to handle complex dynamics and provide smooth control responses is crucial for ensuring the safety and efficiency of aerospace operations.
Advantages of LQR
LQR offers several advantages, making it a popular choice in control system design:
- Optimal Performance: LQR provides optimal control solutions that minimize the defined cost function.
- Robustness: The method is robust against disturbances and uncertainties in system dynamics.
- Simplicity: LQR is relatively easy to implement and computationally efficient, especially for linear systems.
Implementation Techniques
Implementing LQR requires careful consideration of several factors:
- System Modeling: Accurate modeling of the system dynamics is crucial for effective LQR application.
- Choosing Q and R: Selecting appropriate weighting matrices Q and R significantly influences performance.
- Real-time Computation: Efficient algorithms must be employed for real-time control applications.
Challenges of LQR
While LQR is powerful, it is not without challenges:
- Nonlinear Systems: LQR is primarily designed for linear systems; nonlinear dynamics may complicate its application.
- Model Accuracy: The performance of LQR heavily relies on the accuracy of the system model.
Conclusion
In summary, the Linear Quadratic Regulator (LQR) is a fundamental tool in control theory that provides optimal solutions for controlling dynamic systems. Its principles, mathematical foundations, and wide-ranging applications make it an essential topic for engineers and researchers. As you explore LQR further, consider how its principles can be applied to your specific field of interest.
We encourage you to leave a comment below if you have any questions or insights regarding LQR. Don't forget to share this article with others who may find it beneficial!
Thank you for reading, and we invite you to return for more insightful articles on control systems and engineering topics.
Understanding The Role Of Football Receivers: Skills, Techniques, And Impact On The Game
Umpire Eric Gregg: A Comprehensive Look At His Life And Career
Understanding The World Population Of Muslims: Growth, Distribution, And Impact